arxiv: https://arxiv.org/abs/2312.09979
作者提出了一种在 MoE 模型上使用 LoRA 的方法。
论文贡献如下:
- 作者发现大量的微调数据会严重损害 LLMs 在原本学到的知识。保持 LLMs 原本知识与大规模下游数据微调存在冲突。
- 提出一种用 LoRA 训练 MoE 模型的方法。
- LoRAMoE 在多个实验被证明有效。
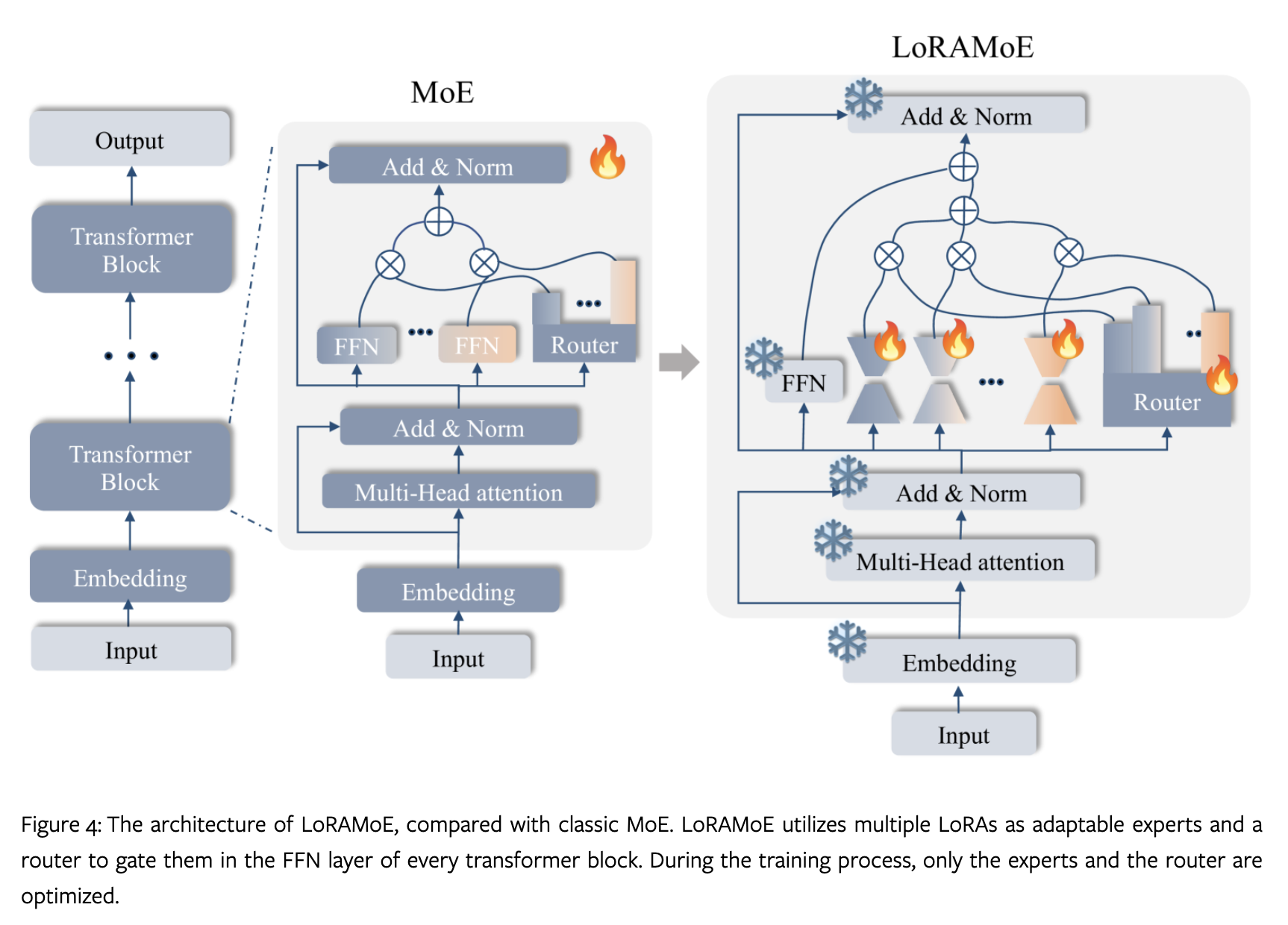
做法也如同上图所示,只需要对 MoE 中的 experts 加上 LoRA,以及对 router 进行微调。
然后这部分是论文的重点:
在 MoE router 计算时,存在一个重要性矩阵 $Q$。 $Q_{n,m}$代表一个 batch 内 $m$ 个训练数据与 $n$ 个experts 的 values的和:
\[Q_{n,m} = \sum_{j=1}^{T_m} G(x_j) \cdot \frac{\exp(\omega_j^T / \tau)}{\sum_{k=1}^N \exp(\omega_k^T / \tau)}\]作者设置了一个相同大小的矩阵$I$作为权重:
\[I_{n,m} = \begin{cases} 1 + \delta, & \text{if } Type_e(n) = Type_s(m) \\ 1 - \delta, & \text{if } Type_e(n) \neq Type_s(m) \end{cases}\]$ I_{n,m} $ 是矩阵 $ I $ 在第 $ n $ 行第 $ m $ 列的元素,代表第 $ n $ 个 expert 对第 $ m $ 个数据的重要性系数。$ \delta $ 是一个介于 0 和 1 之间的参数,用于控制不同 expert 之间的重要性权重。$ Type_e(n) $ 表示第 $ n $ 个 expert 的类型。$ Type_s(m) $ 表示第 $ m $ 个训练数据的任务类型。
如果匹配,则会增加一个 $\delta$ ,反之则会减少一个 $\delta$ 。
作者设计了一个 loss 函数来衡量加权后的重要性矩阵 $Z = I \circ Q$ 的分散程度:
\[\mathcal{L}_{lbc} = \frac{\sigma^2(Z)}{\mu(Z)}\]这样 router 可以确保对一部分 expert 的关注,又不会完全 不关注 其他 expert 。
方差除以均值,通常用来度量分布的离散程度。在概率论和统计学中,这个比值称为离散指数(index of dispersion),变异系数(coefficient of variation),或离散系数(dispersion coefficient),通常用于描述一个概率分布相对于其均值的离散程度。在实际应用中,它可以用来评估数据的波动性或者模型预测的不确定性。
损失函数 $ \mathcal{L}_{lbc} $ 表示了 $ Z $ 的方差和均值的比值。这个比值在统计学中经常用来评估一组数据的变异程度相对于其平均水平的大小。在机器学习或深度学习的上下文中,这个损失函数可能用来鼓励模型输出(由 $ Z $ 表示)具有较低的相对离散性,这可能有助于减少过拟合或提高预测的稳定性。
在实际应用中,$ \mathcal{L}_{lbc} $ 可能用于优化过程,促使模型生成的 $Z $ 矩阵的元素在不同训练样本和专家之间有着相对均衡的贡献,或者确保某种形式的正则化。由于$ Z $是两个矩阵的元素乘积,这也意味着损失函数同时考虑了专家重要性和专家输出的变异性。
最终的 loss 计算如下:
\[\mathcal{L}_{total} = \mathcal{L} + \beta \mathcal{L}_{lbc}\]实验设置如下:
$\beta$ 和 $\delta$ 都设置为0.1,LoRA 中 $\alpha$ 和 $\gamma$ 设置为 32 和 4 ,dropout 0.05, lr 2e-4 。
训练数据 3 million ,在 32张A100 80G上完成训练。
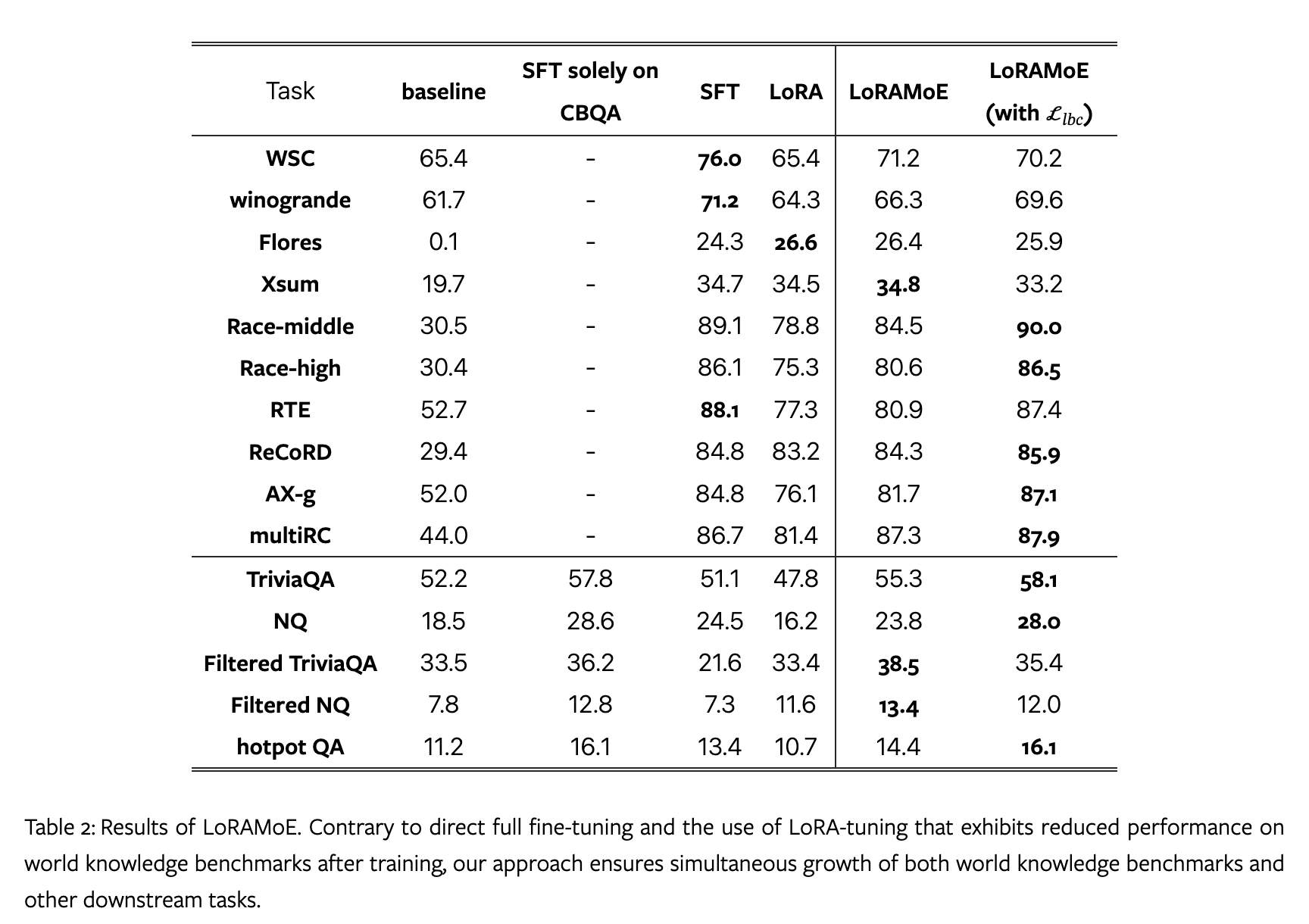
LoRAMoE 在训练后仍然保持了原本的知识,在下游任务上也取得提高。
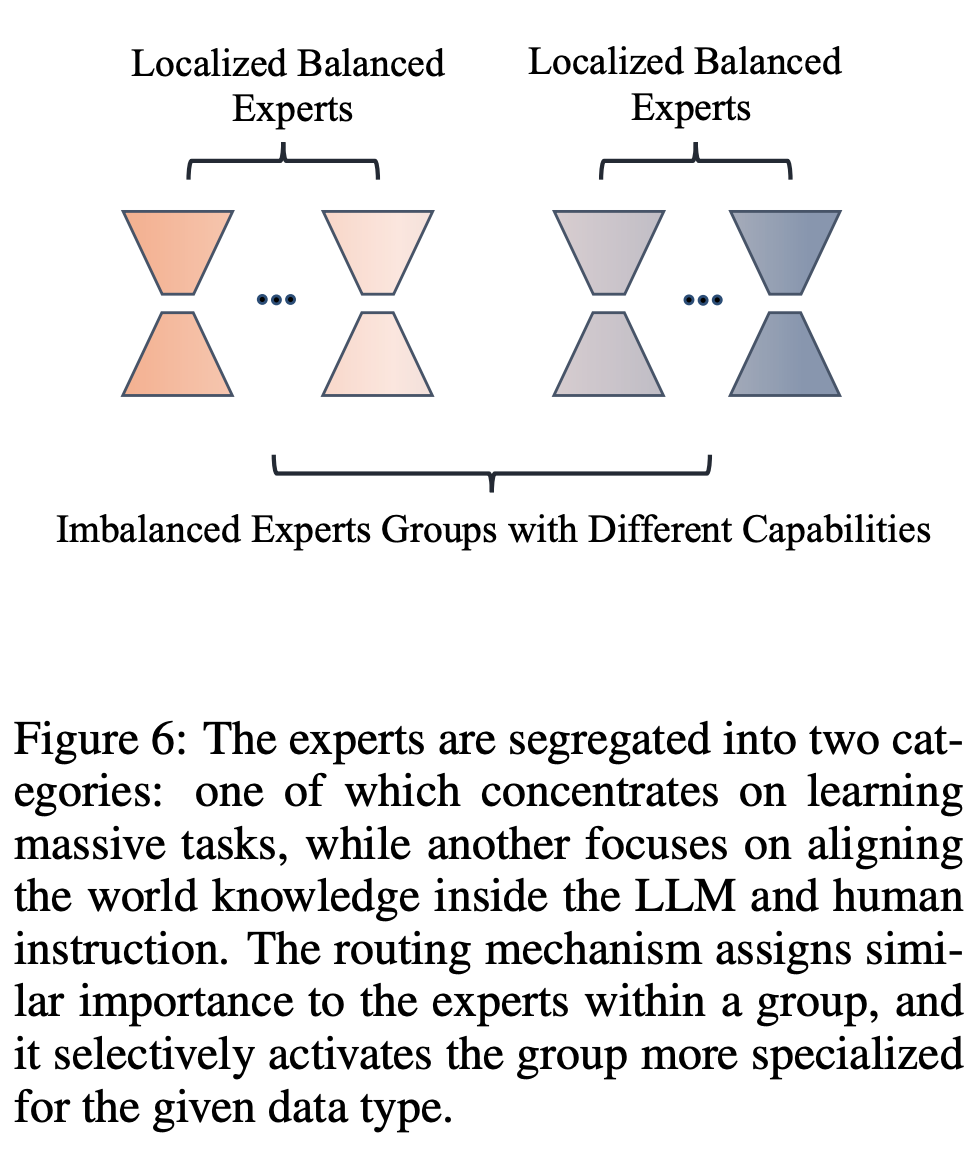
作者对 router 分配上也做了可视化:
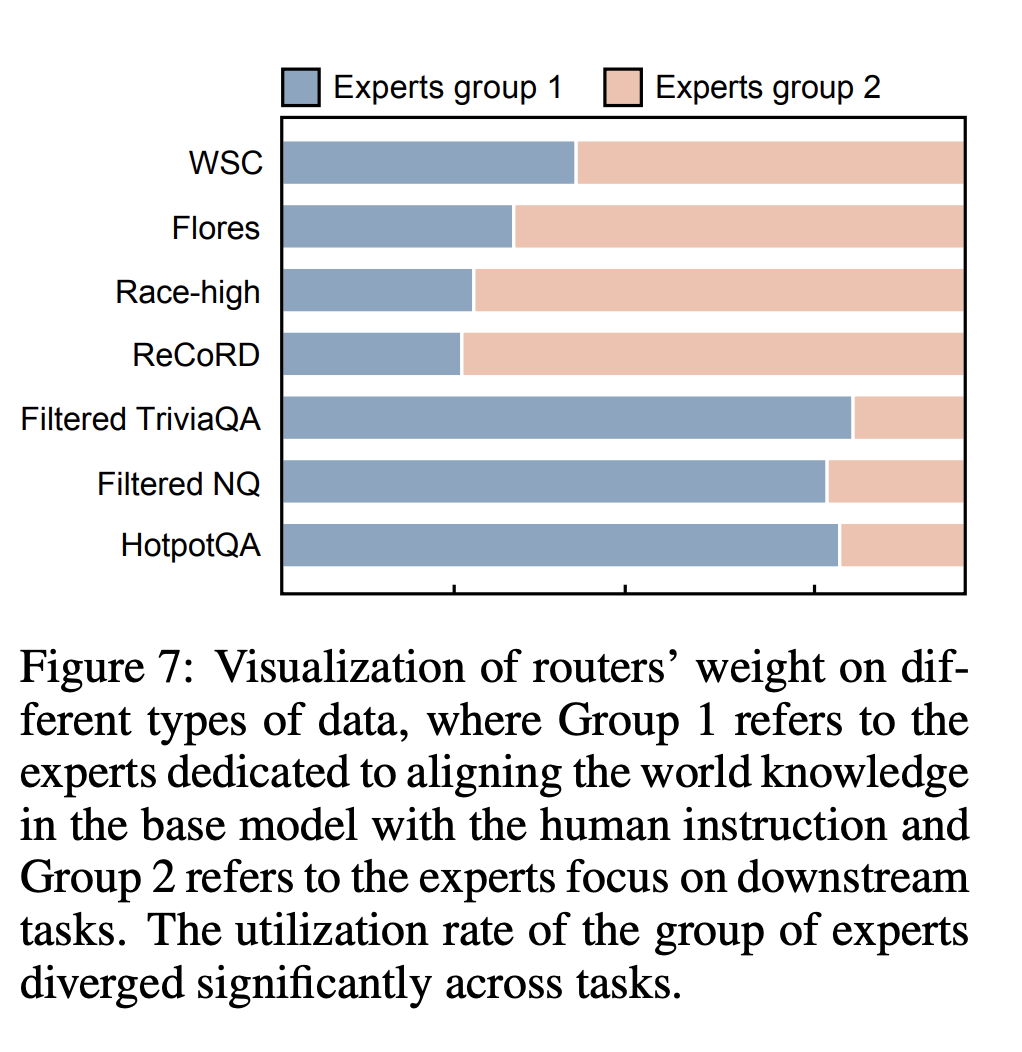
Til next time,
gqjia
at 00:00

